Wprowadzenie do teorii grafów - cz. 1
Niedziela, 24 Maja 2009, 14:18
Czas czytania 4 minuty, 39 sekund
Jest to pierwsza z trzech części artykułu mającego na celu wprowadzenie czytelnika do zagadnienia teorii grafów. Przedstawione tu zostały podstawowe pojęcia i trochę o zastosowaniach grafów.
Wstęp do teorii grafów - cz. 1
Wprowadzenie Witam w pierwszej części artykułu mającego na celu wprowadzenie czytelnika do zagadnienia teorii grafów. Przedstawione tu zostaną podstawowe pojęcia dotyczące grafów, trochę teorii oraz kilka przykładów ich zastosowania. Czyli w skrócie: Z czym to się je. ;)
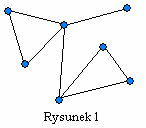
Na początku należy powiedzieć, co to w ogóle jest teoria grafów? Według Wikipedii, jest to dział matematyki zajmujący się badaniem własności grafów. Ale w takim razie czym jest graf? W dużym uproszczeniu, jest to zbiór wierzchołków oraz łączących je krawędzi. Bardziej formalnie jest to pewna struktura danych, czyli sposób uporządkowania informacji w komputerze. Rysunek 1 przedstawia przykładowy spójny graf. Ma on 7 wierzchołków i 8 krawędzi.
Podstawowe pojęcia dotyczące grafów Wiem, że nikt nie lubi masy teorii no ale niestety trzeba się z tym zapoznać. Na szczęście nie będzie tu żadnych pogiętych, wymyślnych nazw tylko bardzo intuicyjne pojęcia. :)
Rodzaje grafów:
Graf spójny - jest to graf w którym poruszając się po krawędziach możemy znaleźć ścieżkę między dowolną parą wierzchołków.
Graf pełny - jest to taki graf w którym każda para wierzchołków jest połączona pojedynczą krawędzią.
Graf acykliczny - jest to graf w którym nie występują żadne cykle, tj. nie mamy żadnej możliwości chodzenia w kółko. :)
Graf skierowany - rodzaj grafu w którym każda krawędź ma swój określony kierunek w którym możemy się po niej poruszać. Przykładowo, jeśli krawędź prowadzi od wierzchołka 2 do wierzchołka 4 to nie możemy jej wykorzystać do podróży z wierzchołka 4 do 2. ;)
Mam nadzieję, że nie muszę wyjaśniać takich pojęć jak graf niespójny, graf cykliczny czy graf nieskierowany. Liczę na waszą wrodzoną inteligencję ;)
Istnieje jeszcze wiele rodzajów grafów jednak nie będę tu ich wszystkich wyjaśniał. Wymieniłem te najważniejsze.
Inne pojęcia:
Cykl - Już przy definicji grafu acyklicznego powiedziałem czym jest cykl, jednak tutaj podam bardziej sztywną definicję. Cykl to droga zamknięta, czyli taka której pierwszy wierzchołek jest jednocześnie ostatnim. Na grafie z rysunku 1 możemy odnaleźć dwa rozłączne cykle.
Waga krawędzi - Krawędziom grafu możemy przypisywać różne wagi. Jest to jakby koszt podróży tą krawędzią.
Stopień wierzchołka - Jest to liczba krawędzi sąsiadujących z wierzchołkiem. W grafach skierowanych możemy wyróżnić stopień wchodzący i wychodzący czyli odpowiednio liczbę krawędzi prowadzących do i wierzchołka z niego wychodzących.
Sąsiad wierzchołka - Jest to wierzchołek połączony z danym wierzchołkiem pojedynczą krawędzią.
Przykłady zastosowania grafów No dobrze, wszystko pięknie, ale po co nam to? Rozważmy następujący problem: Jaś wraca ze szkoły. Jest bardzo zmęczony po ciężkim dniu i chciałby jak najszybciej położyć się w wygodnym łóżku. Chciałby więc dowiedzieć się jaka jest najkrótsza droga ze szkoły do domu prowadząca jedynie po wyznaczonych ścieżkach. Możemy mu powiedzieć, żeby nie marudził i zdrzemną się na jakimś kamieniu, albo możemy przedstawić ten problem w postaci grafu i w ten sposób pomóc Jasiowi w znalezieniu najkrótszej drogi do domu. ;)
Gdybyśmy wszystkie skrzyżowania dróg w miasteczku Jasia potraktowali jako jakieś punkty, natomiast drogi jako krawędzie wychodzące z tych punktów, o wagach równych długości odpowiadających im dróg, uzyskali byśmy graf przedstawiający system dróg w miasteczku. Istnieje tzw. algorytm Dijkstry znajdujący najkrótszą drogę od dowolnego wierzchołka do wszystkich pozostałych.
No, ale co nas obchodzi jakiś Jaś i jego problemy? Jakie korzyści nam dostarczają grafy? Otóż okazuje się, że algorytmy oparte na grafach znajdują wiele praktycznych zastosowań. Przykładowo, możliwość szybkiego wyliczenia najkrótszej drogi przez komputer jest zastosowana w samochodowych GPSach. Wiem, że większość osób czytających ten artykuł to amatorzy programowania gier. Również w tej dziedzinie grafy są nam niezwykle pomocne. Wyobraźmy sobie, że piszemy sztuczną inteligencję postaci sterowanej przez komputer i chcemy by postać ta była w stanie odnaleźć najkrótszą drogę między jakimiś punktami nie wpadając po drodze na ściany, czy inne przeszkody. Wystarczy w odpowiedni sposób przedstawić mapę gry jako graf. Analogicznie możemy zaprogramować inteligentny pocisk omijający przeszkody, albo komputerowego przeciwnika w jakiejś samochodówce.
I to by było na tyle... ...w tej części artykułu. Być może trochę cię zanudziłem, ale wydaje mi się, że to była ta nudniejsza część. Dalej będzie ciekawiej. W następnych częściach opiszę sposoby reprezentacji grafów w programowaniu, oraz kilka podstawowych algorytmów operujących na grafach. Czyli trochę więcej praktyki (oczywiście teorii też nie zabraknie). ;)
Przejdź do następnej części
Wprowadzenie Witam w pierwszej części artykułu mającego na celu wprowadzenie czytelnika do zagadnienia teorii grafów. Przedstawione tu zostaną podstawowe pojęcia dotyczące grafów, trochę teorii oraz kilka przykładów ich zastosowania. Czyli w skrócie: Z czym to się je. ;)
Na początku należy powiedzieć, co to w ogóle jest teoria grafów? Według Wikipedii, jest to dział matematyki zajmujący się badaniem własności grafów. Ale w takim razie czym jest graf? W dużym uproszczeniu, jest to zbiór wierzchołków oraz łączących je krawędzi. Bardziej formalnie jest to pewna struktura danych, czyli sposób uporządkowania informacji w komputerze. Rysunek 1 przedstawia przykładowy spójny graf. Ma on 7 wierzchołków i 8 krawędzi.
Podstawowe pojęcia dotyczące grafów Wiem, że nikt nie lubi masy teorii no ale niestety trzeba się z tym zapoznać. Na szczęście nie będzie tu żadnych pogiętych, wymyślnych nazw tylko bardzo intuicyjne pojęcia. :)
Rodzaje grafów:
Graf spójny - jest to graf w którym poruszając się po krawędziach możemy znaleźć ścieżkę między dowolną parą wierzchołków.
Graf pełny - jest to taki graf w którym każda para wierzchołków jest połączona pojedynczą krawędzią.
Graf acykliczny - jest to graf w którym nie występują żadne cykle, tj. nie mamy żadnej możliwości chodzenia w kółko. :)
Graf skierowany - rodzaj grafu w którym każda krawędź ma swój określony kierunek w którym możemy się po niej poruszać. Przykładowo, jeśli krawędź prowadzi od wierzchołka 2 do wierzchołka 4 to nie możemy jej wykorzystać do podróży z wierzchołka 4 do 2. ;)
Mam nadzieję, że nie muszę wyjaśniać takich pojęć jak graf niespójny, graf cykliczny czy graf nieskierowany. Liczę na waszą wrodzoną inteligencję ;)
Istnieje jeszcze wiele rodzajów grafów jednak nie będę tu ich wszystkich wyjaśniał. Wymieniłem te najważniejsze.
Inne pojęcia:
Cykl - Już przy definicji grafu acyklicznego powiedziałem czym jest cykl, jednak tutaj podam bardziej sztywną definicję. Cykl to droga zamknięta, czyli taka której pierwszy wierzchołek jest jednocześnie ostatnim. Na grafie z rysunku 1 możemy odnaleźć dwa rozłączne cykle.
Waga krawędzi - Krawędziom grafu możemy przypisywać różne wagi. Jest to jakby koszt podróży tą krawędzią.
Stopień wierzchołka - Jest to liczba krawędzi sąsiadujących z wierzchołkiem. W grafach skierowanych możemy wyróżnić stopień wchodzący i wychodzący czyli odpowiednio liczbę krawędzi prowadzących do i wierzchołka z niego wychodzących.
Sąsiad wierzchołka - Jest to wierzchołek połączony z danym wierzchołkiem pojedynczą krawędzią.
Przykłady zastosowania grafów No dobrze, wszystko pięknie, ale po co nam to? Rozważmy następujący problem: Jaś wraca ze szkoły. Jest bardzo zmęczony po ciężkim dniu i chciałby jak najszybciej położyć się w wygodnym łóżku. Chciałby więc dowiedzieć się jaka jest najkrótsza droga ze szkoły do domu prowadząca jedynie po wyznaczonych ścieżkach. Możemy mu powiedzieć, żeby nie marudził i zdrzemną się na jakimś kamieniu, albo możemy przedstawić ten problem w postaci grafu i w ten sposób pomóc Jasiowi w znalezieniu najkrótszej drogi do domu. ;)
Gdybyśmy wszystkie skrzyżowania dróg w miasteczku Jasia potraktowali jako jakieś punkty, natomiast drogi jako krawędzie wychodzące z tych punktów, o wagach równych długości odpowiadających im dróg, uzyskali byśmy graf przedstawiający system dróg w miasteczku. Istnieje tzw. algorytm Dijkstry znajdujący najkrótszą drogę od dowolnego wierzchołka do wszystkich pozostałych.
No, ale co nas obchodzi jakiś Jaś i jego problemy? Jakie korzyści nam dostarczają grafy? Otóż okazuje się, że algorytmy oparte na grafach znajdują wiele praktycznych zastosowań. Przykładowo, możliwość szybkiego wyliczenia najkrótszej drogi przez komputer jest zastosowana w samochodowych GPSach. Wiem, że większość osób czytających ten artykuł to amatorzy programowania gier. Również w tej dziedzinie grafy są nam niezwykle pomocne. Wyobraźmy sobie, że piszemy sztuczną inteligencję postaci sterowanej przez komputer i chcemy by postać ta była w stanie odnaleźć najkrótszą drogę między jakimiś punktami nie wpadając po drodze na ściany, czy inne przeszkody. Wystarczy w odpowiedni sposób przedstawić mapę gry jako graf. Analogicznie możemy zaprogramować inteligentny pocisk omijający przeszkody, albo komputerowego przeciwnika w jakiejś samochodówce.
I to by było na tyle... ...w tej części artykułu. Być może trochę cię zanudziłem, ale wydaje mi się, że to była ta nudniejsza część. Dalej będzie ciekawiej. W następnych częściach opiszę sposoby reprezentacji grafów w programowaniu, oraz kilka podstawowych algorytmów operujących na grafach. Czyli trochę więcej praktyki (oczywiście teorii też nie zabraknie). ;)
Przejdź do następnej części



 Jak znajdę czas
Jak znajdę czas