Wprowadzenie do teorii grafów - cz. 3
Niedziela, 24 Maja 2009, 15:12
Czas czytania 5 minut, 46 sekund
Ostatnia część artykułu mającego na celu wprowadzenie czytelnika do zagadnienia teorii grafów. Opisałem tutaj dwa podstawowe algorytmy operujące na grafach.
Wstęp do teorii grafów - cz. 3
Podstawowe algorytmy grafowe Witam w ostatniej części tego artykułu. Opiszę działanie oraz sposoby implementacji dwóch podstawowych algorytmów operujących na grafach. Jest to DFS i BFS. Przyjemnej lektury. ;)
DFS (Przeszukiwanie w głąb) DFS to skrót od Depth-first search. Algorytm ten jest wykorzystywany w bardzo wielu problemach. Służy do przeglądania kolejnych wierzchołków grafu w taki sposób, że zaczynając od dowolnego wierzchołka (korzenia) poruszamy się w głąb grafu. Gdy znajdziemy się w wierzchołku, od którego nie możemy już dojść do żadnego nieodwiedzonego wcześniej, cofamy się o jeden poziom wyżej i przeglądamy kolejnych sąsiadów. Rysunek 5 przedstawia przebieg algorytmu zaczynając od wierzchołka 1. Na czerwono oznaczono wierzchołki odwiedzone, a na zielono wierzchołek, w którym aktualnie się znajdujemy. Kolejność odwiedzania poszczególnych sąsiadów nie ma znaczenia.
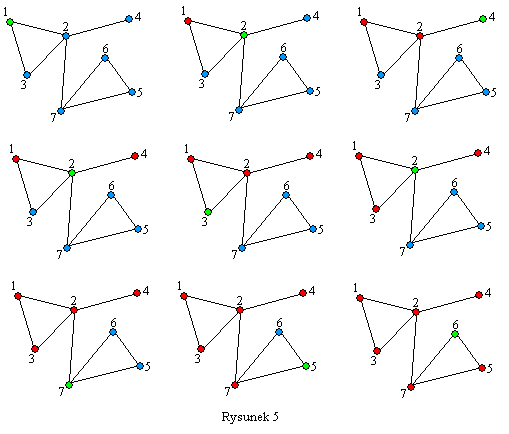
Jak łatwo się domyśleć, w przypadku grafów niespójnych algorytm zakończy swoje działanie przed sprawdzeniem wszystkich wierzchołków. Jest to więc dobry sposób na sprawdzenie spójności grafu.
Implementacja
Najprostszą metodą implementacji DFSa jest zastosowanie rekurencji, czyli wywołania algorytmu wewnątrz samego siebie. Stwórzmy sobie tablicę O, która dla każdego wierzchołka będzie przechowywała wartość 1 jeżeli był on już odwiedzony lub wartość 0 jeżeli nie. Następnie stwórzmy funkcję DFS przyjmującą jeden argument w (numer wierzchołka, od którego zaczynamy przeszukiwanie). Funkcja ta musi aktualnemu wierzchołkowi ustawić wartość w tablicy O na 1 oraz przejrzeć w pętli wszystkich sąsiadów wierzchołka w i wywołać samą siebie dla tych jeszcze nieodwiedzonych.
Tutaj widzimy jak ważna jest odpowiednia reprezentacja grafu. Gdybyśmy wykorzystali macierz sąsiedztwa musielibyśmy za każdym razem przeglądać WSZYSTKIE wierzchołki i sprawdzać czy są połączone z wierzchołkiem w. Listy sąsiedztwa dają nam szybki dostęp do jego sąsiadów.
Złożoność czasowa i pamięciowa
Algorytm wymaga od nas zapamiętania dla każdego wierzchołka czy był on odwiedzany czy nie. Nietrudno, więc zauważyć, że zapotrzebowanie na pamięć jest proporcjonalne do liczby wierzchołków grafu.
Trochę inaczej ma się sprawa złożoności czasowej. Algorytm musi dla każdego wierzchołka grafu sprawdzić wszystkich jego sąsiadów (czy byli już odwiedzani czy nie). Przy reprezentacji grafu za pomocą list sąsiedztwa czas sprawdzania wszystkich sąsiadów będzie, więc proporcjonalny do liczby krawędzi wychodzących z wierzchołka. Widzimy więc, że całkowity czas działania algorytmu będzie proporcjonalny do liczby krawędzi grafu.
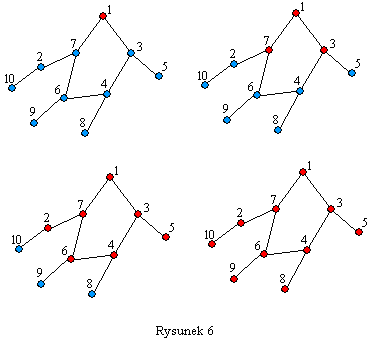
BFS (Przeszukiwanie wszerz) BFS (Breadth-first search) ma bardzo podobne zastosowania co DFS. Również służy do przejrzenia wszystkich wierzchołków grafu jednak obiera trochę inną strategię. DFS najpierw skupiał się na jednym rozgałęzieniu, po czym przechodził do przetwarzania kolejnych. BFS natomiast najpierw sprawdza wszystkich sąsiadów danego wierzchołka, a następnie sąsiadów tych sąsiadów itd. aż do przetworzenia całego grafu. W przykładzie z Rysunku 5 kolejność odwiedzania wierzchołków przy użyciu DFSa była następująca: 1, 2, 4, 3, 7, 5, 6. Przy zastosowaniu algorytmu BFS wierzchołki będą odwiedzane w takiej kolejności: 1, 2, 3, 4, 7, 6, 5. Dla lepszego zrozumienia przeanalizujmy może jeszcze jeden przykład. Rysunek 6 przedstawia przebieg algorytmu dla pewnego grafu.
Implementacja
Tak jak w DFS będziemy potrzebowali pewnej tablicy O przechowującej dla każdego wierzchołka odpowiednią wartość zależnie od tego czy był on już odwiedzony. Dodatkowo utwórzmy sobie kolejkę K zawierającą wierzchołki do odwiedzenia. Na początku znajdować się będzie na niej jedynie wierzchołek początkowy w. Następnie dopóki w kolejce znajdują się jeszcze jakieś nieprzetworzone wierzchołki należy je kolejno zdejmować i przeszukiwać ich sąsiadów. Jeżeli znajdziemy takiego sąsiada, którego jeszcze nie wrzucaliśmy do kolejki (odpowiednia wartość tablicy O jest równa 0) należy to uczynić i zmienić wartość w tablicy O. Przeanalizujemy przebieg algorytmu dla przykładu z Rysunku 6. Na początku w kolejce znajduje się jedynie wierzchołek 1. Ściągamy go i wrzucamy do kolejki wierzchołki 7 i 3. Zdejmujemy 7 i wrzucamy 2 i 6. Nasz kolejka wygląda teraz tak: 3, 2, 6. Bierzemy 3 i wrzucamy do kolejki jej sąsiadów, czyli 4 i 5 (w kolejce mamy: 2, 6, 4, 5). Teraz zdejmujemy 2 itd. Podobnie jak w algorytmie DFS, tak i tutaj korzystna jest reprezentacja grafu przy pomocy list sąsiedztwa.
Złożoność czasowa i pamięciowa
Algorytm BFS oprócz tablicy O wymaga od nas również zapamiętania kolejki nieodwiedzonych dotąd wierzchołków. Złożoność pamięciowa będzie więc istotnie większa niż w algorytmie DFS.
Podobnie jak DFS, BFS musi dla każdego wierzchołka przejrzeć wszystkich jego sąsiadów. Będzie ich tyle ile krawędzi wychodzących z wierzchołka. Złożoność czasowa algorytmu BFS będzie więc również proporcjonalna do całkowitej liczby krawędzi grafu.
Widzimy więc, że algorytm ten jest mniej praktyczny niż DFS. Zwykle wiec się go nie używa. Istnieje jednak klika przypadków, w których BFS może się okazać lepszym rozwiązaniem. Wyobraźmy sobie graf, w którym krawędzie układają się w długi ciąg bez żadnych rozgałęzień. W takim przypadku liczba wywołanych w sobie DFSów była by równa liczbie wszystkich wierzchołków. Dla bardzo dużych danych mogłoby to zaowocować brakiem pamięci.
Przykłady zastosowania-Sprawdzenie spójności grafu
-Wyszukanie najkrótszej drogi od danego wierzchołka do wszystkich pozostałych (pomijając wagi krawędzi)
-Wyznaczenie silnie spójnych składowych grafu skierowanego (jedynie DFS)
-Sortowanie topologiczne (jedynie DFS)
To już jest koniec... ...niniejszego artykułu. Był to jedynie zalążek zagadnienia teorii grafów. Istnieje jeszcze wiele algorytmów wykorzystywanych w różnych problemach, czasami nawet takich, które na pozór nie mają nic wspólnego z grafami. Cieszę się, że dobrnąłeś do tego miejsca. Mam nadzieję, że coś z tej lektury wyniosłeś, że udało mi się przybliżyć ci mniej więcej zagadnienie grafów. Polecam teraz poćwiczyć w praktyce implementacje omówionych tutaj algorytmów. Dziękuję, za przeczytanie mych wypocin :)
Podstawowe algorytmy grafowe Witam w ostatniej części tego artykułu. Opiszę działanie oraz sposoby implementacji dwóch podstawowych algorytmów operujących na grafach. Jest to DFS i BFS. Przyjemnej lektury. ;)
DFS (Przeszukiwanie w głąb) DFS to skrót od Depth-first search. Algorytm ten jest wykorzystywany w bardzo wielu problemach. Służy do przeglądania kolejnych wierzchołków grafu w taki sposób, że zaczynając od dowolnego wierzchołka (korzenia) poruszamy się w głąb grafu. Gdy znajdziemy się w wierzchołku, od którego nie możemy już dojść do żadnego nieodwiedzonego wcześniej, cofamy się o jeden poziom wyżej i przeglądamy kolejnych sąsiadów. Rysunek 5 przedstawia przebieg algorytmu zaczynając od wierzchołka 1. Na czerwono oznaczono wierzchołki odwiedzone, a na zielono wierzchołek, w którym aktualnie się znajdujemy. Kolejność odwiedzania poszczególnych sąsiadów nie ma znaczenia.
Jak łatwo się domyśleć, w przypadku grafów niespójnych algorytm zakończy swoje działanie przed sprawdzeniem wszystkich wierzchołków. Jest to więc dobry sposób na sprawdzenie spójności grafu.
Implementacja
Najprostszą metodą implementacji DFSa jest zastosowanie rekurencji, czyli wywołania algorytmu wewnątrz samego siebie. Stwórzmy sobie tablicę O, która dla każdego wierzchołka będzie przechowywała wartość 1 jeżeli był on już odwiedzony lub wartość 0 jeżeli nie. Następnie stwórzmy funkcję DFS przyjmującą jeden argument w (numer wierzchołka, od którego zaczynamy przeszukiwanie). Funkcja ta musi aktualnemu wierzchołkowi ustawić wartość w tablicy O na 1 oraz przejrzeć w pętli wszystkich sąsiadów wierzchołka w i wywołać samą siebie dla tych jeszcze nieodwiedzonych.
Tutaj widzimy jak ważna jest odpowiednia reprezentacja grafu. Gdybyśmy wykorzystali macierz sąsiedztwa musielibyśmy za każdym razem przeglądać WSZYSTKIE wierzchołki i sprawdzać czy są połączone z wierzchołkiem w. Listy sąsiedztwa dają nam szybki dostęp do jego sąsiadów.
Złożoność czasowa i pamięciowa
Algorytm wymaga od nas zapamiętania dla każdego wierzchołka czy był on odwiedzany czy nie. Nietrudno, więc zauważyć, że zapotrzebowanie na pamięć jest proporcjonalne do liczby wierzchołków grafu.
Trochę inaczej ma się sprawa złożoności czasowej. Algorytm musi dla każdego wierzchołka grafu sprawdzić wszystkich jego sąsiadów (czy byli już odwiedzani czy nie). Przy reprezentacji grafu za pomocą list sąsiedztwa czas sprawdzania wszystkich sąsiadów będzie, więc proporcjonalny do liczby krawędzi wychodzących z wierzchołka. Widzimy więc, że całkowity czas działania algorytmu będzie proporcjonalny do liczby krawędzi grafu.
BFS (Przeszukiwanie wszerz) BFS (Breadth-first search) ma bardzo podobne zastosowania co DFS. Również służy do przejrzenia wszystkich wierzchołków grafu jednak obiera trochę inną strategię. DFS najpierw skupiał się na jednym rozgałęzieniu, po czym przechodził do przetwarzania kolejnych. BFS natomiast najpierw sprawdza wszystkich sąsiadów danego wierzchołka, a następnie sąsiadów tych sąsiadów itd. aż do przetworzenia całego grafu. W przykładzie z Rysunku 5 kolejność odwiedzania wierzchołków przy użyciu DFSa była następująca: 1, 2, 4, 3, 7, 5, 6. Przy zastosowaniu algorytmu BFS wierzchołki będą odwiedzane w takiej kolejności: 1, 2, 3, 4, 7, 6, 5. Dla lepszego zrozumienia przeanalizujmy może jeszcze jeden przykład. Rysunek 6 przedstawia przebieg algorytmu dla pewnego grafu.
Implementacja
Tak jak w DFS będziemy potrzebowali pewnej tablicy O przechowującej dla każdego wierzchołka odpowiednią wartość zależnie od tego czy był on już odwiedzony. Dodatkowo utwórzmy sobie kolejkę K zawierającą wierzchołki do odwiedzenia. Na początku znajdować się będzie na niej jedynie wierzchołek początkowy w. Następnie dopóki w kolejce znajdują się jeszcze jakieś nieprzetworzone wierzchołki należy je kolejno zdejmować i przeszukiwać ich sąsiadów. Jeżeli znajdziemy takiego sąsiada, którego jeszcze nie wrzucaliśmy do kolejki (odpowiednia wartość tablicy O jest równa 0) należy to uczynić i zmienić wartość w tablicy O. Przeanalizujemy przebieg algorytmu dla przykładu z Rysunku 6. Na początku w kolejce znajduje się jedynie wierzchołek 1. Ściągamy go i wrzucamy do kolejki wierzchołki 7 i 3. Zdejmujemy 7 i wrzucamy 2 i 6. Nasz kolejka wygląda teraz tak: 3, 2, 6. Bierzemy 3 i wrzucamy do kolejki jej sąsiadów, czyli 4 i 5 (w kolejce mamy: 2, 6, 4, 5). Teraz zdejmujemy 2 itd. Podobnie jak w algorytmie DFS, tak i tutaj korzystna jest reprezentacja grafu przy pomocy list sąsiedztwa.
Złożoność czasowa i pamięciowa
Algorytm BFS oprócz tablicy O wymaga od nas również zapamiętania kolejki nieodwiedzonych dotąd wierzchołków. Złożoność pamięciowa będzie więc istotnie większa niż w algorytmie DFS.
Podobnie jak DFS, BFS musi dla każdego wierzchołka przejrzeć wszystkich jego sąsiadów. Będzie ich tyle ile krawędzi wychodzących z wierzchołka. Złożoność czasowa algorytmu BFS będzie więc również proporcjonalna do całkowitej liczby krawędzi grafu.
Widzimy więc, że algorytm ten jest mniej praktyczny niż DFS. Zwykle wiec się go nie używa. Istnieje jednak klika przypadków, w których BFS może się okazać lepszym rozwiązaniem. Wyobraźmy sobie graf, w którym krawędzie układają się w długi ciąg bez żadnych rozgałęzień. W takim przypadku liczba wywołanych w sobie DFSów była by równa liczbie wszystkich wierzchołków. Dla bardzo dużych danych mogłoby to zaowocować brakiem pamięci.
Przykłady zastosowania-Sprawdzenie spójności grafu
-Wyszukanie najkrótszej drogi od danego wierzchołka do wszystkich pozostałych (pomijając wagi krawędzi)
-Wyznaczenie silnie spójnych składowych grafu skierowanego (jedynie DFS)
-Sortowanie topologiczne (jedynie DFS)
To już jest koniec... ...niniejszego artykułu. Był to jedynie zalążek zagadnienia teorii grafów. Istnieje jeszcze wiele algorytmów wykorzystywanych w różnych problemach, czasami nawet takich, które na pozór nie mają nic wspólnego z grafami. Cieszę się, że dobrnąłeś do tego miejsca. Mam nadzieję, że coś z tej lektury wyniosłeś, że udało mi się przybliżyć ci mniej więcej zagadnienie grafów. Polecam teraz poćwiczyć w praktyce implementacje omówionych tutaj algorytmów. Dziękuję, za przeczytanie mych wypocin :)